«Для ответа на нужный вопрос подходящих данных нет, а имеющиеся — не нужны» Фраза в одной из книг по занимательной физике
Почему мы взяли для этой части такой эпиграф? Дело в том, что очень часто желающие посвятить себя такой трудной нише, как разработка компьютерных игр пытаются бросаться с места в карьер. Многие же книги по этому поводу написаны с «высоты полета» разработчиков, и они упускают ряд промежуточных, но важных связующих факторов, считая их понимание априори имеющимся в наличие у читателя. Поэтому мы пойдем по более сложному пути, который не основан на бездумном «нажмите это — получите то», а попытаемся привить осознанность собственных действий.
Специфика графических средств разработки современных компьютерных игр заключается в передаче и/или эмуляции трехмерного мира на 2D-плоскости, коей является экран компьютерного монитора. В кино и видео ситуация обстоит иначе. Там намного проще, ведь камера просто фиксирует события внешнего мира, а в нашем случае этот мир нужно полностью создавать. Отдельно стоит отметить, что даже современные пользовательские программные интерфейсы предусматривают некое наличие психологического обмана. Достаточно вспомнить период появления Windows 95 и новых сред разработки, в рамках которых появились новые «объемные» кнопки и другие интерфейсные элементы, предусматривающие эту технологию. С точки зрения игр, такая новация не представляла из себя чего-то особенно нового, поскольку в их рамках уже давно экспериментировали с тенями, посему то, что реально делалось исключительно в 2D плоскости нередко ощущалась трехмерным. На самом деле психология имеет очень большое значение. Возвращаясь к тому же Windows можно сказать, что пользователи действительно ощущают моменты нажатия на кнопки, как будто бы они реальны. Нужно отметить, что реализация такой трехмерности в то время увлекало очень много профессионалов от программирования, причем не только в рамках создания новых компонент, но и получения уникальных и красивых меню с великолепно выглядящими шрифтами. Кстати, стоит отметить, что шрифты в то время стоили дорого, если их приобретать, поэтому очень часто такую работу гораздо выгоднее было делать самостоятельно.
На данный момент практика того времени не является устаревшей, даже более того, до сих пор не редко используется. На рисунке показаны простейшие примеры создания объемных элементов, таких как кнопки и текст. При желании можете поэкспериментировать самостоятельно, используя обычную программу Paint из Windows. Причем такие элементы в рамках программ реализовывались совершенно различными методами. Один из них подразумевал сохранение в одном графическом файле множество рисунков для всех состояний объекта, после чего при появлении определенных событий, это изображение просто меняло координаты, а пользователь видел необходимый результат. Эта техника стала именоваться спрайтовой. Как ее разновидность можно назвать вариант использования множества различных графических файлов для отображения состояний одного объекта. То есть, при появлении какого-либо влияющего события изменялись не координаты большого изображения, а подгружались графические файлы. Причем это нашло некое отображение и в других областях, например, в создании красочных HTML-страниц, а в Adobe Flash такая реализация есть в рамках объектов типа Button. Кстати, по этому методу достаточно часто сейчас делают меню и для игр. Нередко можно встретить ситуацию, когда делаются отдельные рисунки для всех возможных состояний всего меню, и они подгружаются как кадры. Отдельно об этом вопросе мы поговорим досконально и обстоятельно чуть позже. Для начала поговорим о стереовидении и о восприятии объема.
Наше восприятие объема
Почему мы начали разговор об объеме именно с примера с тенями? Для описания этого момента проще ориентироваться на те основы, которые мы излагали в материалах по цифровому видео и компьютерной анимации, причем эти сведения вы должны полностью себе представлять. Многие слышали о параллаксе, могут примерно сказать, как у нас работает система стереовидения, определяя дальность до того или иного объекта. И все это будет по изученным книжкам. А на самом деле просто прикройте один глаз рукой. И что, все вокруг нас потеряло объем, мы не можем определить какой объект ближе, узнать его примерные размеры? Можем. Глядя на картины, или играя в игры с 3D-анимацией на обычном дисплее, мы представляем это как нечто плоское? Отнюдь. Ключевым в последнем вопросе является слово «представляем». Ведь на самом деле глаза — это просто сенсорная система, а за анализ всех поступающих данных отвечает мозг. И в этом случае лучше применять понятие объемного восприятия, которое базируется на множестве различных составных, и стерео (бинокулярное) зрение является лишь вершиной айсберга. Да, объясняя его, можно сказать, что расположенные на некотором расстоянии друг от друга глаза, дают два изображения, мозг их совмещает и, в результате анализа мы получаем представление об объеме и пространстве, мало того, у каждого глаза есть своя оптическая ось, соответственно, как происходит примерное определение дальности расположения того или иного объекта, может вам рассказать любой школьник, изучающий геометрию. Но, все не совсем так как кажется. Даже глядя на все одним глазом, человек может анализировать такие вещи как тени, изменения цветов, сравнение с другими предметами. Если такой наблюдатель проходит мимо какого-нибудь объекта, то может анализировать неравномерное смещение предметов. В принципе, он и получает те же несколько проекций, которые потом мозг «наращивает» до нужного объема. И, кстати, именно, благодаря такому методу птицы также могут видеть, вернее, воспринимать все в объеме. А в общем и целом все то, что мы имеем из технологий сейчас и касается зрительного восприятия — это технологии обмана, как глаз, так и мозга. Звучит немного страшно, но это так.
Многослойная структура 2D и переход к 3D
Даже глядя на обычную двухмерную анимацию, мы мыслим объемно, то есть, анализируем, что за чем стоит. В принципе, 2D-анимация и создаются точно таким же образом. То есть, существует слой главного персонажа, множество других и на заднем плане находится фон.
Почему мы затронули именно этот вопрос при обсуждении темы создания современных компьютерных игр, и тем более, уже вооружившись Direct3D. Дело в том, что слои отсчитываются в сторону и в глубину от пользователя. То есть, если в рамках обычного моделирования, изучаемого в той же школе на уроках черчения (если такой еще есть), представляя трехмерную проекцию, мы виртуально направляем ось Z на нас, то есть, от листа бумаги, то в играх мы будем ее направлять от нас, то есть вглубь. Технологически это называется правосторонней и левосторонней системой координат, в нашем случае — левосторонняя. То есть, мы смотрим, как и виртуальная камера.
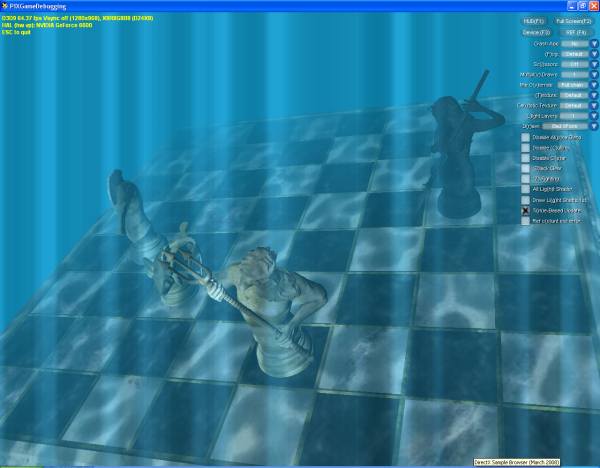
В качестве наглядного примера многослойности в первую очередь и самой эффективности применения левосторонней системы координат, в директории установленного DirectX SDK откройте проект Microsoft DirectX SDK\Samples\C++\Direct3D\Tutorials\PIXGameDebugging. Покрутите шахматную доску указателем мыши. При этом вы видим что первый слой муара является статическим ни на что не влияющим. При этом подумайте, а как бы это можно было реализовать в рамках 2D-анимации. Правильно! Нужно просто менять геометрические формы и размеры всех объектов по определенному закону, а при вращении показывать только видимые для камеры элементы. Причем сам элемент хранится как определенный сложный объект, имеющий множество составляющих. Данные обрабатываются и преобразуются. В принципе, в этом и есть весь внутренний смысл трехмерной анимации. И не стоит пугаться сложности представленного примера, при желании, скоро вы сможете самостоятельно делать множество подобного.
Эксперименты в 2D... Что показано на рисунке?
Простой и достаточно иллюстративный пример-опыт. Представим, что мы находимся на самой заре компьютерной мультимедийной эры (в начале 90-х, а то и намного раньше), и перед нами стоит задача сделать интерактивные шарообразные элементы (не мелкие). Цель — они должны восприниматься объемно и изменять блик от света в процессе движения, а также масштабироваться. Выше мы рассматривали наше восприятие объема, то есть оно осуществляется мозгом при анализе множества составляющих, среди которых для нашего случая сначала используем тень, то есть, понадобится специализированная закраска. Конечно, резонно было бы предположить, что все можно реализовать и на уровне точек (пиксельная графика), то есть, представить объект как их множество, собранное по определенному математическому закону, и при каждом движении рассчитывать цвета. Ход мыслей верный, но на самом деле это подразумевает огромный пласт трудоемких расчетов. Поэтому проще разбить объект на определенное количество графических примитивов — полигонов. Рисуя треугольник (или многоугольник) на плоскости, мы обозначили границы некоторой области. Точки, находящиеся внутри оной принадлежат этой фигуре и подчиняются единому для нее закону, например, по закраске. Создав объект из полигонов-примитивов мы тем самым аппроксимируем (упрощаем) его представление. Первый вертикальный ряд на рисунке — создание объекта из четырехугольников. С их помощью мы получили многогранник, издалека напоминающий окружность. После этого начинаем делать закраску элементов в однотонные цвета, изначально предположив, что источник света находится справа сверху. Для простоты эксперимента используем только четыре цвета: белый, светло-серый, темно-серый и черный. Что-то получилось. Причем мы использовали инструмент "Заливка" и справились с задачей за 10 секунд, а представьте сколько бы времени ушло на закраску каждой точки... Причем после закраски объект начинает выглядеть объемно только за счет нашего представления о тенях. Возвращаемся к перечислению составляющих нашего объемного восприятия вспоминаем: анализ изменения пропорций. Предположим, что наблюдатель или объект двигается. Следовательно, все графические примитивы последнего должны поменять пропорции своих сторон по определенному закону. Делается это программно, но в данном случае мы смоделируем одну из ситуаций, сместив опорную точку (назовем ее так) нашей модели на некоторое расстояние. Закрасим все, согласно тому, как это было раньше. Что получилось в итоге? Наш «шар», конечно, отказался выглядеть как шар, и стал похож на прямоугольный контейнер. Но при этом мы видим изменения объемной фигуры. Что делать с формой объекта? Нужно разбивать его на большее количество примитивов. Во втором вертикальном ряду рисунка вы видите, как сказалось разбиение четырехугольников на треугольники. Мы получили нечто пикообразное, но оно уже воспринимается как круглый предмет, это очень хорошо. Разбиваем дальше. Из рисунка вы видите, что чем больше элементов мы внедряем (разбиваем на большее количество составных примитивов), тем более реалистичным становится наш шар, и на контейнер он уже совсем не похож. И в данном случае практически чистым рисованием мы из плоской фигуры только за счет различного изменения пропорций примитивов (составных элементов — трех- и четырехугольников) можем подчеркнуть характер объема общей фигуры. Например, сделать из нее конус, полусферу и т. п. В последнем вертикальном ряду рисунка показан некий фрагмент неровной поверхности. Вы видите, что, смещая нашу опорную точку и изменяя пропорции примитивов по специальным законам, можно достичь весьма реалистичного результата. То есть, что можно вынести из данного примера в качестве выводов: наличие теней и изменения пропорций примитивов могут указать на качество и характер объемности моделируемого объекта. В принципе, как задаются пропорции, вернее алгоритмы их изменения должно быть понятно, самое главное, что видно даже из этих рисунков, все составные элементы проектируемой модели связаны по вершинам. В нижнем правом углу иллюстрации вы еще можете увидеть метод изменения формы предметов с сопутствующим изменением форм примитивов и их окраски. На самом деле, скажем вот что:). Ваш покорный слуга рисовал этот рисунок в программе Paint около часа, просто решил вспомнить часть молодости, проведенной за математическим моделированием объемных графических объектов. В то время о 3D ходили только слухи на уровне суперкомпьютеров и фразы «виртуальная реальность», которая являлась чем-то фантастическим. И представьте, сколько времени могло уйти, например, на построение математической модели отображения сферы, либо еще более сложного объекта, с последующим перенесением в программный код, внесением коэффициентов по изменению пропорций при движении и так далее. По существу, я в то время практически с нуля создавал программу двумерного отображения движущихся трехмерных объектов (то есть их можно было вращать, передвигать и т.п.), и, кстати, не одну, поскольку каждый 3D-объект требовал написания отдельной программы. Причем на данном примере мы фактически работали с полусферой, а для полноценного объема к ней нужно виртуально подсоединить вторую такую же сзади, а при повороте объемной фигуры уже анализировать, какие из примитивов должны быть видимы и как, а какие нет, причем изменение пропорций будет другим. Вот так непросто. Сейчас для того, чтобы получить нарисованный результат, вам достаточно открыть любой пакет создания трехмерной анимации и создать сферу, выбрав соответствующий инструмент. Это займет около минуты. Градации цвета и тени у вас будут расставляться автоматически с помощью специальных программных модулей.
На самом деле в *.х файлах хранятся только координаты вершин, а сетку из треугольных примитивов Direct3D строит самостоятельно
Отдельно хочется отметить, что любую объемную поверхность можно описать примитивами, за единицу такового в Direct3D из геометрических фигур принято считать треугольник (в OpenGL используются любые многоугольники). Причем в ряде 3D-пакетов объемные поверхности часто формируются и отображаются также, как и в нашем примере, то есть совокупностью треугольников и четырехугольников. На самом же деле, большую важность представляют собой не такие примитивы как полигоны, которые могут быть различными, а вершины, то есть точки. Многие из тех, кто уже далеко продвинулся дальше, спросят о том, а как же происходит тот же экспорт моделей из профессиональных пакетов в формат Direct3D (файлы с расширением *.x), если при их проектировании в 3D-пакетах явно присутствуют четырехугольные полигоны. На самом деле все просто, чтобы убедиться в этом откройте файл с расширением *.x в текстовом редакторе (Блокноте). Что вы увидите? Правильно, просто список координат вершин. А уже в свою очередь Direct3D все самостоятельно дробит на треугольники. Насчет оптимизации таких моделей поговорим в последующих материалах.
Сглаживание и свойства человеческого зрения
Вспоминая давние игры, в которых впервые стали использовать примитивы для создания сложных трехмерных объектов стоит отметить, что последние там смотрелись весьма угловато и неправдоподобно. Почему это так происходило, вы могли увидеть уже на описанном выше примере — чем на большее количество примитивов разбивается модель, тем более естественно она воспринимается. Первые трехмерные объекты в играх смотрелись очень угловато и неестественно. Это ощущение имеет место по двум существенным причинам. Во-первых, человеческий глаз может детализировать все окружающие предметы до одной угловой минуты, далее все сливается. Таким образом, вы не можете рассмотреть каждый кирпич в далеко расположенном здании, а на экранах мониторов не видите каждый отдельный пиксель (ЖКИ) либо строчку (ЭЛТ). Но системы из треугольников ранней эпохи предусматривали гораздо меньший предел детализации, то есть, вы могли отчетливо рассмотреть каждый элемент (треугольник), причем даже шар, нарисованный нами, при достаточно близком рассмотрении выглядел как многогранник. То есть, нужны, говоря хорошим языком, элементы градации формы. А по существу, речь идет об улучшенной детализации. Во-вторых, сглаживание. Если вы рассмотрите поближе пиксельное изображение, то оно покажется вам также неестественным, а что уж говорить об объектах, каждая грань которых предусматривает резкий переход от одного цвета к другому. Сглаживание реализуется различными путями, но основной из них — добавление промежуточных элементов изменения градации цвета. И хотя с цветом особенно для линий, графических элементов и точек все решается и обычными методами antialiasing (сглаживание), такой предусмотрен и в DirectX, на этом все прелести и заканчиваются. То есть, внутреннюю структуру моделей все равно нужно усложнять, то есть при необходимости дробить треугольники на малые, добавлять градиентные составляющие и так далее. Как это реализуется в компьютерных играх? Мы знаем что, чем больше полигонов, тем лучше, но тогда на обработку такого объекта будет уходить очень много машинных ресурсов. Поэтому в рамках каждой сцены рассчитывается дальность (обычно три уровня) по уровням детализации, также можно применить понятие «планов», известных нам из кино и видео, а в игровой терминологии применяется понятие «плоскостей проекций». В рамках той, которая расположена ближе всего к пользователю загружаются модели с максимальной детализацией (самым большим числом полигонов), на среднем плане — со средней детализацией, на дальнем — с минимальной. То есть, на самом деле 3D-моделлеры каждую из моделей готовят в трех видах с различной детализацией (иногда в двух). Как это увидеть наиболее наглядно? Очень просто. Возьмите какую-нибудь экономическую стратегию с видом сверху. Покрутите колесико мыши, измените масштаб от самого крупного до самого мелкого. Посмотрите как меняется детализация движущихся объектов на дорогах и т.п. И в большинстве случаев то, что раньше в играх выводилось на передний план, на современном уровне годится только для среднего и дальнего. Уровень детализации неуклонно растет, а количество полигонов уже может исчисляться миллионами для каждого отдельного персонажа.
Так как же хранятся трехмерные объекты?
Вы думаете это реальная машина? Нет, это трехмерная модель дизайнера Pascal Wenzel, созданная в Maxon Cinema 4D
На самом деле, многие ошибочно полагают, что программы 3D-моделирования «понимают», что такое объем, трехмерность и так далее. Отнюдь. Это понимает человек, а данный софт разработан как инструментарий для удобства нашего собственного восприятия. То есть, можно сказать и так, что любой 3D-объект является многомерным массивом со своей внутренней структурой. Хранит он в себе ничто иное как данные обо всех взаимосвязанных примитивах. В предыдущем примере мы рассматривали вариант рисования трехмерного объекта на 2D-плоскости, описать который можно координатами X и Y вершин, могли даже его программировать, но в действительности вы будете работать с трехмерной системой координат, что подразумевает свою уже удобную и отработанную организацию рабочего процесса. То есть, очень много работы уже сделали за вас. Это и правильно, и неправильно одновременно. Потому как на чужом движке, или чужом алгоритмическом ядре для своего движка (будем считать его высокоуровневым) вы не напишете программы, которые будут работать с такой же легкостью, как лучшие разработки мира. С другой стороны сама скорость разработки имеет очень важное значение, поэтому иногда без чужого не обойтись. В рамках каждой трехмерной сцены на базе ее геометрического описания формируется изображение в 2D. Происходит это с помощью системы последовательных действий, именуемых конвейером визуализации (rendering pipeline). Об этом мы будем говорить подробно и не раз.
Примитивы в Direct3D
Чтобы материал не выглядел совсем уж теоретическим, возьмемся за практику, то есть, уже будет над чем поработать и вам. Помимо треугольника в Direct3D предусмотрено еще два типа примитивов, а именно, линия и точка. Их мы в учет принимать не будем. Еще треугольники, кроме закрепившимся за ними постыдного понятия «примитивы», по общепринятой терминологии могут называться полигонами или ячейками сетки. Почему сетки, думается, вам понятно, ведь «внутри» все так и выглядит. Это уже потом мы ее начинаем закрашивать, нанизывать определенную текстуру, добавляем освещение, создаем тени. То есть, работы хватает. Итак, смотрим на структуру примитива под именем треугольник, он состоит из трех вершин и трех граней. Вершины могут подразумевать под собой не только координаты собственного месторасположения, то есть, это не просто математический термин, Direct3D наделяет их дополнительными особыми свойствами. Формат представления вершин позволяет к самим координатам добавлять множество дополнительных данных, к примеру, информацию о цвете, нормали, координатах текстуры. Сам же формат вершин является достаточно гибким. Он так и называется Flexible Vertex Format (FVF). Давайте рассмотрим конкретный пример. Чтобы создать собственный формат вершин, изначально создаем структуру:
struct MYVERTEX { FLOAT x, y, z; // Задаем координаты месторасположения DWORD color; // Задаем цвет };
После этого нам нужно описать формат хранения с помощью комбинации флагов FVF, а именно:
#define FVF_COLOR (D3DFVF_XYZ | D3DFVF_DIFFUSE)
То есть, то, что вы задаете, потом просто описывается флагами. Какие бывают их доступные разновидности можно найти в документации DirectX SDK с поиском по ключевому слову «D3DFVF». Кстати, я неспроста не(!) стал опираться на пример вывода треугольника по вершинам из уроков Direct3D (можно найти в установленном SDK в директории: …\Microsoft DirectX SDK\Samples\C++\Direct3D\Tutorials\Tut02_Vertices). На самом деле там очень небольшой и простой листинг, но вместо флага D3DFVF_XYZ используется D3DFVF_XYZRHW и формат задается соответственно. В чем их различие предлагаю разобраться самостоятельно. И в конце этого материала условимся на том, что основные кирпичики трехмерной графики — это все-таки не треугольники, а вершины.
Кристофер Перепечатка материалов или их фрагментов возможна только с согласия автора.
|